ДИНАМИКА БЛОХОВСКОЙ ДОМЕННОЙ ГРАНИЦЫ. ТЕОРИЯ И ЭКСПЕРИМЕНТ

Теория динамики доменной границы
Изучение динамики доменной границы в пленке феррита-граната под действием импульсного магнитного поля.
- Упражнение 1. Метод однократной фотографии
- Упражнение 2. Метод двукратной фотографии. Определение подвижности ДГ
Вопросы к задаче
Список литературы
Калькулятор

Цель настоящей работы познакомиться с особенностями динамики блоховской доменной границы. Для достижения этой цели будут решены следующие задачи:

используя уравнение Ландау-Лифшица, будет получена теоретическая зависимость скорости движения блоховской доменной границы от величины внешнего магнитного поля и проведено сравнение структуры статической и динамической доменной границы;
по фотографиям динамической доменной границы, полученных с помощью методов однократной и двукратной высокоскоростной фотографии, будут построены зависимость смещения доменной границы от времени и зависимость скорости движения границы от величины внешнего магнитного поля;
экспериментально полученное значение подвижности доменной границы будет сопоставлено с расчетным значением.

Теория динамики доменной границы.

Фундаментальным исходным уравнением при теоретическом анализе динамики доменной границы является предложенное Ландау и Лифшицем уравнение движения магнитного момента M. Для краткости сразу запишем его с релаксационным членом в форме Гильберта применительно к системе, изображённой на Рис. 1:

\[\frac{\partial\vec M}{\partial t}=\gamma\left[\vec H_{эфф}\times\vec M\right]+\frac{\alpha}{M_0}\left[\vec M\times\frac{\partial\vec M}{\partial t}\right], \vec H_{эфф}=-\frac{\delta F}{\delta M} ,\] \[ F=A\left[\left(\frac{\partial\theta}{\partial y}\right)^2+\left(\frac{\partial\varphi}{\partial y}\right)^2 \sin^2\theta \right] + K\sin^2\theta+2\pi M_0 \sin^2\theta \sin^2\varphi-M_0 H\cos\theta ,\]

(1)

где γ – гиромагнитное отношения для электрона, α – параметр затухания, F – свободная энергия, состоящая из слагаемых: обменной энергии, энергии анизотропии, энергии размагничивающего поля и Зеемановской энергии соответственно, A – константа обменного взаимодействия, K – константа анизотропии.

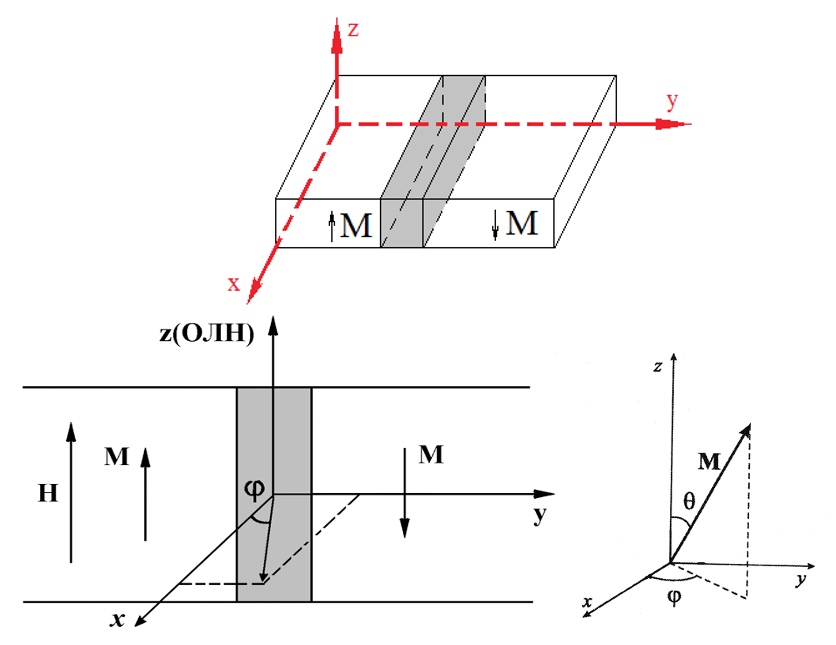
Рис. 1: Бесконечная блоховская доменная граница во внешнем магнитном поле Н: М – намагниченность в соседних доменах; θ, φ – угловые координаты.

В 1935 г. в работе Ландау и Лифшица была впервые разработана теория движения одномерной блоховской доменной границы в пределе малых скоростей и получено линейное соотношение между скоростью границы и полем, которое ориентировано вдоль оси лёгкого намагничивания. Дальнейшее развитие теория получила в работе Уокера, который нашёл точное решение для случая образца с одноосной магнитной анизотропией.

В сферических координатах (угловых координатах θ и φ) уравнение Ландау-Лифшица в форме Гильберта (1) может быть сведено к системе из двух уравнений:

\[\begin{cases} \dot\theta+\alpha\dot\varphi\sin\theta=\omega_m\sin\theta\sin\varphi\cos\varphi+\frac{\omega_m Q\delta_0^2}{\sin⁡\theta}\frac{\partial}{\partial y}\left(\sin^2\theta\frac{\partial\varphi}{\partial y}\right) ,\\ -\alpha\dot\theta+\dot\varphi\sin\theta=\omega_m\sin\theta\cos\theta\sin^2\varphi+\omega_m Q\sin\theta\cos⁡\theta+ \gamma H\sin\theta+\omega_m Q \delta_0^2\left[\sin\theta\cos\theta\left(\frac{\partial\varphi}{\partial y}\right)^2-\left(\frac{\partial^2\theta}{\partial y^2}\right)\right] , \end{cases}\]

(2)

где $\omega_m=4\pi\gamma M_0$ и $\delta_0=\sqrt{A⁄K}$. Решение (1) ищем в виде $\varphi=\varphi(t), \theta=\theta(\xi(t))$:

\[ \xi(t)=\frac{y(t)-q(t)}{\delta(\varphi)} , \delta(\varphi)=\frac{\delta_0}{\sqrt{1+\sin^2\varphi⁄Q}} ,\]

(3)

где $q(t)$ – смещение доменной границы под действием поля, $Q=K⁄(2\pi M_0^2)$ – фактор качества материала.

Поскольку производные по времени от углов θ и φ связаны между собой (2), структура динамической доменной границы отличается от структуры статической, в частности, тем, что в процессе движения границы магнитные моменты отклоняются относительно плоскости стенки на угол φ=const, т.е. ориентация намагниченности внутри ДГ зависит не только от одной координаты. Исходя из этих соображений, в 1963 г. Уокером было получено стационарное решение (1) ($y=Vt$, $\varphi(t)=0$):

\[ V(H)=\frac{\mu H}{\sqrt{1+\sin^2\varphi⁄Q}} , \mu=\frac{\gamma\delta_0}{\alpha} ,\] \[ \varphi=\frac12\arcsin\frac{H}{H_W} , H_W=2\pi\alpha M_0 ,\]

(4)

где $\mu$ – подвижность доменной границы, $H_W$ – критическое поле Уокера. Зависимость скорости движения ДГ от величины внешнего поля можно переписать в явном виде, используя полученные выражения (4):

\[ V(H)=\frac{V_W H\sqrt{1+\frac{1}{2Q}}}{H_W\sqrt{1+\frac{1}{2Q}(1-\sqrt{1-(H⁄H_W)^2}) }} . \]

(5)

Решение (4) существует только при условии $H\le H_W$. В полях, превышающих поле Уокера стационарного движения не существует.

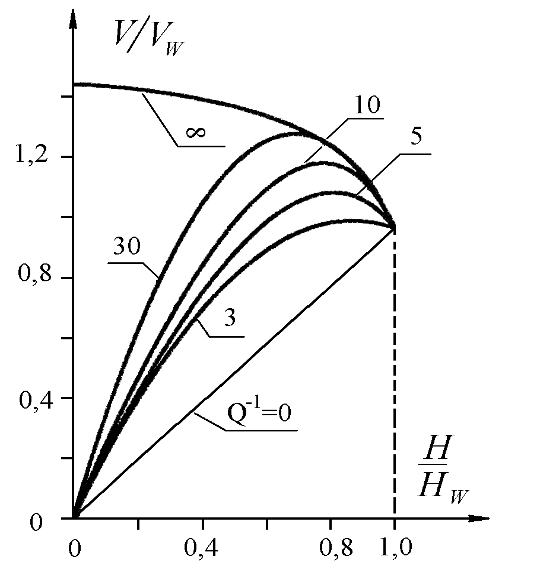
Рис. 2: Зависимость относительной скорости стационарного движения доменной границы от приведенной величины внешнего магнитного поля при различных значениях фактора качества Q.

На Рис. 2 представлены рассчитанные по формуле (5) для разных $Q$ зависимости $V(H)$; их нелинейный характер при $Q^{-1}>1$ объясняется динамическим уменьшением ширины стенки по мере возрастания $H$. Если $Q\to\infty$ ($Q^{-1}\to 0$), то вплоть до $H=H_W$ скорость доменной границы будет линейно зависеть от продвигающего поля $H$:

\[ V(H)=\mu H , \mu=\frac{\gamma\delta_0}{\alpha} .\]

(6)

Скорость доменной границы в поле Уокера называется критической скоростью Уокера:

\[ V_W=2\pi\gamma\delta_0⁄\sqrt{1+1/(2Q)} .\]

(7)

Когда $Q\gg1$, то задача о динамике блоховской доменной границы значительно упрощается. Структура границы определяется тогда, в первую очередь, обменным взаимодействием и анизотропией (как и в случае статической блоховской доменной границы), а силы магнитостатического происхождения и силы, связанные с действием внешнего поля и с динамической реакцией, являются поправками. В результате ширина границы не меняется при движении, а, следовательно, не меняется и её подвижность.

\[ \delta(\varphi)=\frac{\delta_0}{\sqrt{1+\sin^2⁡\varphi⁄Q}}=\frac{\delta_0}{\sqrt{1+\frac{1}{2Q}\left(1-\sqrt{1-(H⁄H_W)^2}\right)}} .\]

(8)

Наименьшая толщина доменной границы наблюдается при её движении в поле Уокера $H=H_W$:

\[ \delta_{\mathrm{min}}(\varphi)=\delta_0/\sqrt{1+\frac{1}{2Q}} .\]

(9)

Помимо критической скорости стационарного движения доменная граница может обладать и максимальной (предельной) скоростью стационарного движения $V_m$:

\[ V_m=2\gamma\sqrt{2\pi A}\,\, (Q\ll 1) .\]

(10)

В полях, превышающих поле Уокера ($H>H_W$), доменная граница движется вдоль оси $y$, совершая колебательные движения (Рис. 3). При этом структура доменной границы периодически меняется от блоховской к неелевской и обратно.

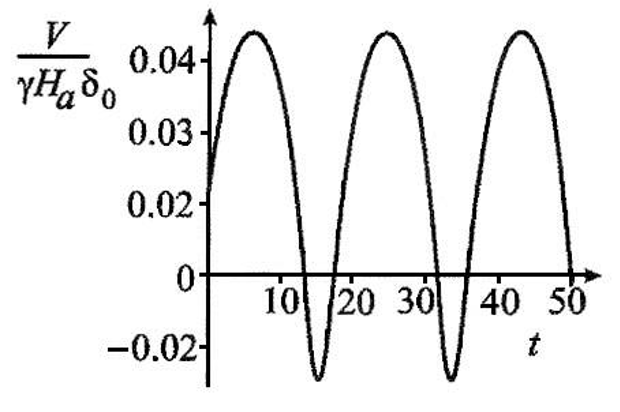
Скорость доменной границы от времени в полях превышающих поле Уокера

Рис. 3: Зависимость скорости движения доменной границы от времени. Результаты расчетов для $\alpha=0.1$ и $Q=10$, $H/H_W=2$.

Выражение для скорости доменной границы в этом случае можно записать в виде:

\[ V=2\pi\gamma M_0 \delta_0 \frac{\alpha^2}{1+\alpha^2}\left(\frac{H}{H_W}+\frac{H_W}{\alpha^2\left(H+\sqrt{H^2-H_W^2}\right)}\right) .\]

(11)

Впервые эта зависимость была получена Слончевским в 1972 г. Независимо, другими методами эту зависимость получили Хуберт (1977), а также Раев и Ходенков (1981).

На Рис.4а представлены кривые $V(H)$, рассчитанные по формуле (10) для разных значений параметра $\alpha$. На всех зависимостях после начального линейного участка есть область с отрицательной подвижностью. При $\alpha=0.2$ в больших полях наблюдается рост скорости, при этом скорость ДГ не превышает скорость Уокера. На Рис.4б показана экспериментальная зависимость $V(H)$, полученная методом двукратной высокоскоростной фотографии. Эта зависимость соответствует кривым, представленным на Рис.4а.

Можно записать подвижность доменной границы в области сильных полей ($\tilde\mu$) и найти связь между подвижностью в сильных и слабых полях:

\[ \tilde\mu=\frac{\alpha\delta_0\gamma}{1+\alpha^2}\,(H\ll H_W), \; \tilde\mu=\alpha^2\mu . \]

(12)

Поскольку под действием магнитного поля, превышающего поле Уокера, внутренняя структура доменной границы периодически меняется, энергия внешнего магнитного поля, управляющего движением границы, расходуется не только на ее продвижение, но и на стабилизацию ее структуры. Именно этим объясняется наличие участка с отрицательной дифференциальной подвижностью на зависимости $V(H)$. Из выражения для скорости доменной границы (5) можно увидеть, что максимальная скорость достигается при $H\le H_W$, а при $H>H_W$ существует область с отрицательной дифференциальной подвижностью, где скорость с ростом поля уменьшается (Рис. 4 а,б).

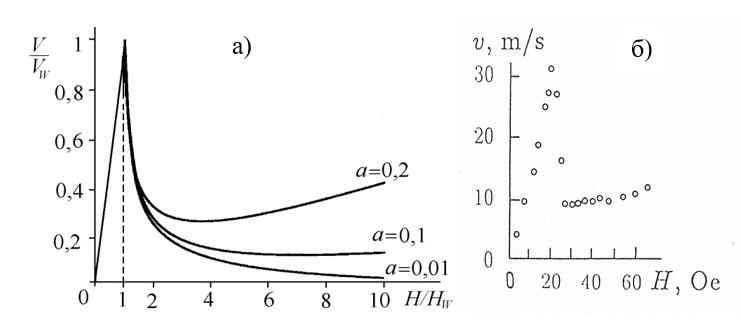
Рис. 4: (а) Зависимость скорости движения ДГ от внешнего магнитного поля для различных значений параметра затухания ($Q\to\infty$) [1], (б) Экспериментальная зависимость скорости движения доменной границы в пленках феррита-граната от величины магнитного поля [2].

В начало $\uparrow$

Изучение динамики доменной границы в пленке феррита-граната под действием импульсного магнитного поля

Упражнение 1. Метод однократной фотографии

Для исследования динамики доменных границ (ДГ) могут быть использованы разные методы: метод Сикстуса-Тонкса и его магнитооптический аналог, метод коллапса цилиндрических магнитных доменов, методы однократной и двукратной высокоскоростной фотографии [2], метод, основанный на эффекте Холла [3], а также метод, в котором используется дифракция света на доменной структуре [4]. Увидеть динамическую доменную границу позволяют только методы высокоскоростной фотографии.

В настоящем разделе для определения скорости движения ДГ будет использован метод однократной высокоскоростной фотографии. Схема установки показана на Рис. 5.

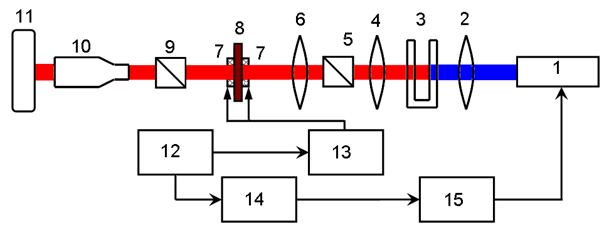
Рис. 5: Схема экспериментальной установки для исследования динамики доменных границ методом однократной высокоскоростной фотографии 1 − импульсный лазер, 2, 4, 6 − линзы, 3− кювета с красителем, 5 − поляризатор, 7 − катушки, создающие продвигающее магнитное поле, 8 − образец, 9 − анализатор, 10 − микроскоп, 11 − фотокамера, 12 − запускающий генератор, 13 − генератор импульсов тока, 14− генератор, 15− блок питания лазера.

Работа лазера (1) синхронизирована с работой генератора (13), с помощью которого создается импульсное магнитное поле в катушках (7), расположенных на образце (8). Работа системы в целом синхронизирована так, что камера (11) фиксирует состояние системы в определенный момент времени. Изменяя задержку между импульсом света и импульсом тока, можно получить серию фотографий динамической доменной границы. После обработки этих фотографий можно получить зависимость смещения ДГ от времени и вычислить значение максимальной скорости.

Рис. 6: Лабиринтная доменная структура в пленке феррита-граната. Намагниченность в соседних доменах ориентирована перпендикулярно поверхности пленки.

Длительность импульса света в эксперименте может составлять от десятков фемтосекунд до сотен пикосекунд. В настоящем эксперименте длительность световых импульсов была 150 фс.

Известно, что в пленке феррита-граната в отсутствие внешнего магнитного поля реализуется лабиринтная доменная структура (Рис. 6), намагниченность в соседних доменах ориентирована перпендикулярно поверхности пленки. Для создания в образце единственной ДГ и гарантии повторяемости экспериментов, положение единственной доменной границы в образце стабилизируют с помощью градиентного магнитного поля (Рис. 7). Для создания этого поля в эксперименте обычно используют постоянные магниты. В настоящем эксперименте величина этого поля была 3,3 кЭ/см, ее не меняли в процессе измерений. Наряду с перпендикулярной компонентой $H_z$ градиентное магнитное поле имеет и плоскостную компоненту, ориентированную в плоскости образца перпендикулярно плоскости ДГ $H_y^\parallel$.

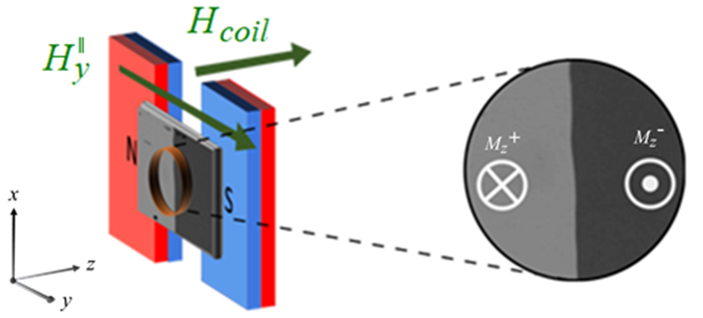
Рис. 7: Использование градиентного магнитного поля для создания в пленке феррита-граната единственной доменной границы. $M_z^\pm$ – намагниченность в доменах, направленная перпендикулярно плоскости образца от наблюдателя и на него. $H_y^\parallel$ - плоскостная компонента магнитного поля, создаваемого постоянными магнитами. Соленоид на поверхности образца, создает импульсное магнитное поле $H_\mathrm{coil}$, запускающее движение доменной границы.

На Рис. 8 представлены однократные фотографии динамической доменной границы в моменты времени t1=0 (а) и t2=1 мкс (б) с начала действия импульса поля с амплитудой 200 Э. Размер кадра по вертикали (1400 делений) – 1,28 мм. Выбрав неподвижные дефекты на поверхности образца, можно определить координату ДГ (y) в разные моменты времени (t) и, обработав серию фотографий, получить зависимость y(t). По начальному линейному участку этой зависимости можно определить скорость движения границы.

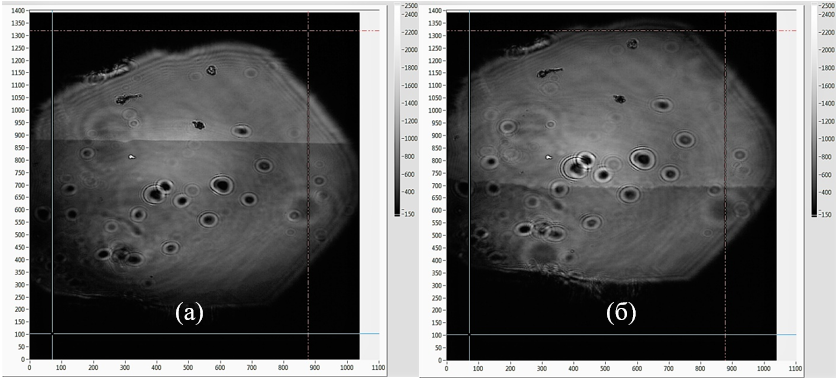
Рис. 8: Однократные фотографии динамической доменной границы в момент времени $t_1=0$ (а) и $t_2=1$ мкс (б) с начала действия импульса поля с амплитудой 200 Э. Размер кадра по вертикали (1400 делений) 1,28 мм.

В этом упражнении, необходимо:

определить величину плоскостной компоненты постоянного магнитного поля, создаваемого градиентными магнитами $H_y^\parallel$;
получить зависимость смещения ДГ под действием прямоугольного импульса магнитного поля от времени $y(t)$;
используя эту зависимость, определить скорость движения доменной границы $V$;
провести моделирование динамики ДГ при ее движении из положения равновесия.

В начало $\uparrow$

Экспериментальная часть

1.1 Определение плоскостной компоненты градиентного магнитного поля

На Рис. 9 показана геометрия системы, состоящей из немагнитной подложки (выделена синим), образца (выделен зеленым) и постоянных магнитов, создающих градиентное магнитное поле, (серые). Зная зависимость компоненты градиентного магнитного поля $H_z$ на нижней поверхности образца в точке с координатами $(0,0,a)$ от координаты $y$ $H_z$ $(0,y,a)=G\cdot y$, где $G$ – величина градиентного магнитного поля ($G$=3,3 кЭ/см), можно определить компоненту этого поля в точке $H_y$ $(0,0,a)$, предполагая, что его создают равные по модулю магнитные заряды ($q_{11l}=q_{12l}=⋯=q_{42r}$), расположенные в точках, выделенных на Рис. 9 красным цветом.

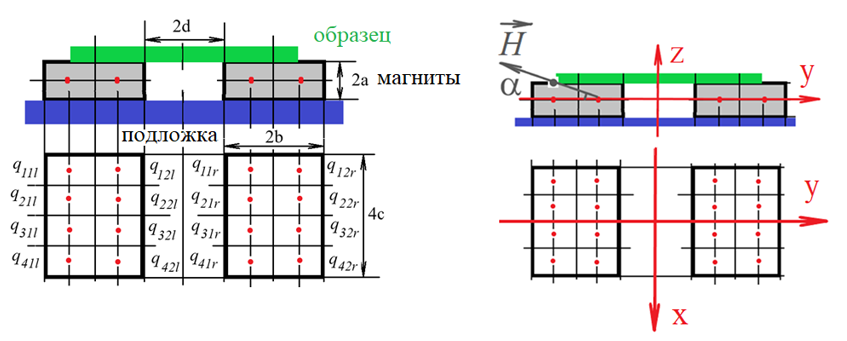
Рис. 9: Геометрия системы: 2a=2мм; a=1мм; 2b=6мм; b=3мм; 4c=12мм; c=3мм; 2d=3мм; d=1.5мм.

1.2 Получение зависимости координаты доменной границы от времени и вычисление скорости движения границы

Для получения зависимости смещения доменной границы из положения равновесия от времени необходимо по каждому изображению из папки «однократные фотографии» (ссылка на фотографии дана в конце описания) провести не менее трех измерений. На фотографии следует выбрать несколько дефектов, положение которых не меняется. Пример такого выбора показан на Рис. 10. Измеряя расстояния между выбранными точками и доменной границей, можно получить зависимость расстояния, пройденного доменной границей, от времени. Для удобства следует считать, что в начальный момент времени доменная граница находится в точке с координатой $y$=0.

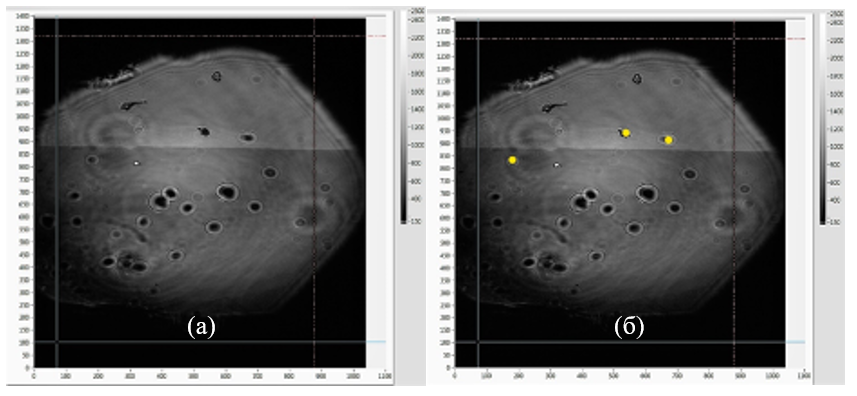
Рис. 10: Пример выбора неподвижных точек для измерений смещения доменной границы из положения равновесия: (а) – исходная фотография (б) – та же фотография с выделенными желтым цветом неподвижными дефектами, относительно которых будет измерена координата доменной границы.

В названии фотографий содержится информация о том, в какой момент времени с начала действия импульса магнитного поля они сделаны. Например, фотография «Garnet_mobility_200Oe_0.4us» была получена через 0,4 мкс после начала действия импульса магнитного поля с амплитудой 200 Э. В этой серии фотографий амплитуда импульса магнитного поля была постоянна.

По начальному участку зависимости $y(t)$ можно определить величину скорости движения доменной границы, соответствующую амплитуде импульса магнитного поля.

1.3 Моделирование динамики доменной границы под действием импульсного и градиентного магнитного полей

Ранее уже было отмечено, что градиентное магнитное поле стабилизирует начальное положение доменной границы. На Рис. 11а схематично показана зависимость компоненты градиентного магнитного поля $H_z$ от координаты $y$ в геометрии, представленной на Рис. 9. Импульсное магнитное поле, создаваемое в катушках, которые расположены на поверхностях образца, приводит к смещению границы из положения равновесия. В той области образца, где происходит движение ДГ, магнитное поле, создаваемое катушками, можно считать не зависящим от координат $x$ и $y$. Таким образом, суммарное поле, действующее на доменную границу в начальный момент времени, зависит от координаты $y$ так, как показано на Рис. 11б и может быть описано соотношением: $H_z(y)=G\cdot y–H_\mathrm{coil}$, где $G$=3,3 кЭ/см – градиентное магнитное поле. Максимальное смещение доменной границы из положения равновесия определяется величинами градиентного и импульсного магнитных полей. В точке $y_\mathrm{max}$, где $H_z(y_\mathrm{max})$=0, доменная граница остановится. $y_\mathrm{max}=H_\mathrm{coil}⁄G$.

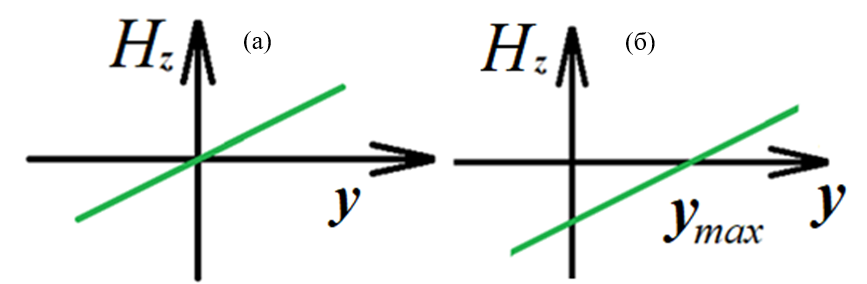
Зависимость компоненты градиентного магнитного поля от координаты

Рис. 11: Зависимость компоненты градиентного магнитного поля, перпендикулярной плоскости образца, от координаты $y$: в отсутствие и в присутствии импульсного магнитного поля (а) и (б) соответственно.

Уравнение движения доменной границы имеет вид: $m\dot V=F$, где $F$ – сила, действующая на доменную границу, $m$ – ее масса. Поскольку сила, продвигающая доменную границу, пропорциональна внешнему магнитному полю, уравнение движения границы можно записать в виде:

\[ m\dot V=C(G\cdot y-H_\mathrm{coil}) ,\]

(13)

где $C$ – коэффициент пропорциональности, имеющий размерность [Н/Э]. Левую часть уравнения можно преобразовать, используя соотношения:

\[ \frac{dV}{dt}=\frac{dV}{dy}\cdot\frac{dy}{dt}=V\frac{dV}{dy} .\]

(14)

Тогда уравнение движения ДГ будет иметь вид:

\[ mV\frac{dV}{dy}=C(G\cdot y-H_\mathrm{coil}) .\]

(15)

Для получения теоретической зависимости смещения ДГ из положения равновесия от времени необходимо решить задачу Коши с условиями:

\[\begin{cases} mV\frac{dV}{dy}=C(G\cdot y-H_\mathrm{coil}) \\ y(t=0)=0 \\ V(y_\mathrm{max}=H_\mathrm{coil}/G)=0) \end{cases}.\]

(16)

Результаты расчетов представьте в виде зависимости $V(y)$ и $y(t)$. Последнюю зависимость можно преобразовать к виду $y(t)⁄y_\mathrm{max}$ и сравнить с аналогичной экспериментальной кривой, полученной в п.1.2.

В начало $\uparrow$

Упражнение 2. Метод двукратной фотографии. Определение подвижности ДГ

Метод двукратной фотографии, основанный на эффекте Фарадея – уникальный метод исследования динамики доменных границ в прозрачных ферромагнетиках [2]. В отличие от метода однократной фотографии, для определения величины скорости движения ДГ достаточно одной фотографии динамической доменной границы, что значительно повышает эффективность работы.

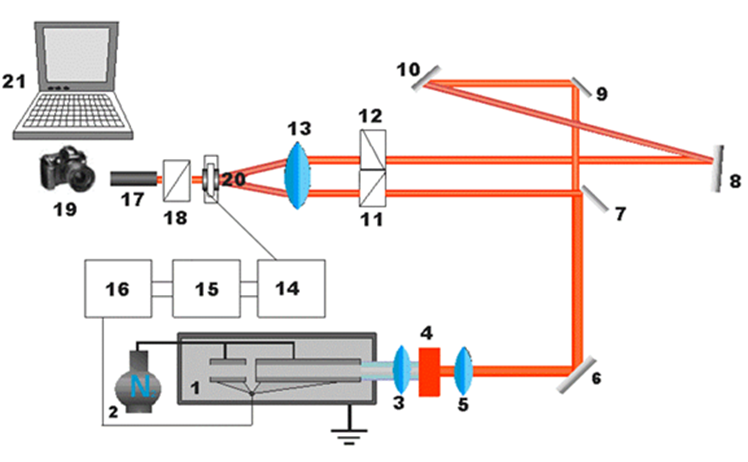
Рис. 12: Схема экспериментальной установки для исследования динамики доменных границ методом двукратной высокоскоростной фотографии. 1 – лазер; 2 – сосуд Дьюара с азотом; 3, 5,13– линзы; 4 – кювета с красителем; 6 – 10 – зеркала; 11,12 – поляризаторы; 14 – генератор, подающий импульсы тока в катушки, 15 – запускающий генератор, 16 – блок питания лазера, 17 – микроскоп, 18 – анализатор; 19 – фотокамера; 20 – образец; 21 – компьютер.

Схема установки для реализации этого метода показана на Рис. 12. Свет от импульсного лазера (1) с помощью зеркала (7) разделяют на два луча одинаковой интенсивности. Динамическую доменную границу в образце (20) освещают двумя световыми импульсами. Один из них с помощью системы зеркал (8-10) задержан относительно другого. Разность хода между лучами 30 см создает задержку между световыми импульсами 1 нс. Обычно в эксперименте задержка между двумя световыми импульсами может составлять от нескольких наносекунд до нескольких десятков наносекунд. Ее величину устанавливают в зависимости от характерных скоростей движения ДГ в материале: чем больше скорость движения, тем меньше задержка между световыми импульсами. Длительность одного импульса света может составлять от десятков фемтосекунд до сотен пикосекунд. В настоящем эксперименте длительность световых импульсов составляла 250 пс, задержка между двумя импульсами (630 нм) составляла 13 нс.

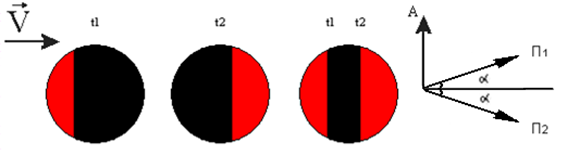
Рис. 13: Схема получения контраста двукратных фотографий «в контрасте доменов». Доменная граница движется слева направо. Первый луч фиксирует положение динамической доменной границы в момент времени $t_1$, второй луч – в момент времени $t_2$. Темная полоса на двукратной фотографии – расстояние, пройденное доменной границей за интервал времени между световыми импульсами. В правой части рисунка показано взаимное расположение главных осей поляризаторов П1 и П2 и анализатора А. На Рис. 12 поляризаторы П1 и П2 – обозначены (11) и (12), а анализатор – (18).

Первый и второй луч проходят через поляризаторы (11) и (12) соответственно и анализатор (18). Главные оси поляризаторов и анализатора устанавливают так, чтобы изображения доменной структуры, полученные с помощью первого и второго луча, были обратны (Рис. 13). При наложении изображений доменной структуры, полученных в моменты времени $t_1$ и $t_2$, на фотографии получается темная полоса, ширина которой $S$ – расстояние, пройденное доменной границей за интервал времени между двумя световыми импульсами. Зная задержку между световыми импульсами $t_1$ и $t_2$, можно определить скорость движения доменной границы:

\[ V=\frac{S}{t_2-t_1} .\]

(17)

Положение единственной доменной границы в этом эксперименте фиксируют с помощью градиентного магнитного поля 6 кЭ/см. Доменная граница движется под действием импульсного магнитного поля, создаваемого с помощью соосных катушек с внутренним диаметром 1-2 мм, которые расположены на поверхностях образца. Управляя временем задержки между световыми импульсами и импульсом продвигающего магнитного поля, можно получить изображения динамической доменной границы в разные моменты времени.

Работа оптической системы синхронизирована с работой генератора, создающего импульсное магнитное поле в катушках. Это является гарантией того, что на одной двукратной фотографии будут последовательно зафиксированы два положения доменной границы, движение которой вызвано одним импульсом магнитного поля.

В настоящем упражнении необходимо:

определить скорость движения доменной границы по фотографиям, полученным для разных величин импульсных магнитных полей и построить зависимость скорости движения доменной границы от величины внешнего магнитного поля $V(H_\mathrm{coil})$;
вычислить значение подвижности доменной границы $\mu_э$;
используя значения параметров пленок ферритов-гранатов из работы [5], вычислить максимальное и минимальное значение подвижности и сравнить с ранее полученным результатом.

2.1 Определение зависимости скорости движения доменной границы от величины импульсного магнитного поля и вычисление подвижности

Для получения зависимости скорости движения доменной границы от величины импульсного магнитного поля по фотографиям, необходимо определить скорость движения ДГ и величину импульсного поля. Пример двукратной фотографии показан на Рис. 14. На всех фотографиях этой серии граница движется справа налево. Горизонтальный размер всех фотографий 470 мкм. Задержка между первым и вторым импульсами света 13 нс, длительность каждого импульса света 1/4 нс. Величина импульсного магнитного поля указана в названии фотографии. Например, фотография «32.7Oe-1» получена в присутствии импульсного магнитного поля с амплитудой 32,7 Э.

Рис. 14: Двукратная фотография динамической доменной границы в пленке феррита-граната. Граница движется справа налево под действием импульсного магнитного поля с амплитудой 78,5 Э. Задержка между первым и вторым импульсами света 13 нс.

По результатам измерений можно построить зависимость скорости движения доменной границы $V$ от величины импульсного поля $H_\mathrm{coil}$. Начальный участок зависимости $V(H_\mathrm{coil})$ описывается линейной функцией:

\[ V=\mu\cdot H_\mathrm{coil} ,\]

(18)

где $\mu$ – подвижность доменной границы.

В начало $\uparrow$

Вопросы к задаче

В первом упражнении необходимо:

определить величину плоскостной компоненты постоянного магнитного поля, создаваемого градиентными магнитами $H_y^\parallel$ (п. 1.1);
по однократным фотографиям динамической доменной границы получить зависимость смещения границы под действием импульса магнитного поля от времени $y(t)$ (п. 1.2);
по начальному линейному участку этой зависимости, определить скорость движения доменной границы $V$ (п. 1.2);
провести моделирование динамики доменной границы под действием градиентного и импульсного магнитного полей ДГ при ее движении из положения равновесия (п. 1.3). Результаты расчетов представьте в виде зависимостей $V(y)$ и $y(t)$. Последнюю зависимость можно преобразовать к виду $y(t)⁄y_\mathrm{max}$ и сравнить с аналогичной экспериментальной кривой, полученной в п.1.2.

Во втором упражнении необходимо:

определить скорость движения доменной границы по двукратным фотографиям, полученным для разных величин импульсных магнитных полей, и построить зависимость скорости движения доменной границы от величины внешнего магнитного поля $V(H_\mathrm{coil})$;
вычислить значение подвижности доменной границы $\mu_э$;
используя значения параметров пленок ферритов-гранатов из работы [5], вычислить максимальное и минимальное значение подвижности и сравнить с ранее полученным результатом.