Блоховская доменная граница
Оглавление
- I. Энергии взаимодействия в ферромагнетиках.
- II. Образование доменной структуры в ферромагнетиках.
- III. Переходные слои между доменами. Доменные границы.
- IV. Расчет ширины блоховской доменной стенки.
- Список литературы
- Вопросы к задаче.
- Калькулятор.
I. Энергии взаимодействия в ферромагнетиках.
Магнитное состояние ферромагнетика определяется следующими основными типами энергий взаимодействия:
- Электростатической энергией обменного взаимодействия:
- Энергией естественной или кристаллографическомагнитной анизотропии, которая для одноосного кристалла с гексагональной кристаллической решёткой (например, кобальта) имеет вид:
- Магнитоупругой энергией, связанной с самопроизвольной деформацией кристалла при намагничивании (магнитострикцией) или при прикладывании внешних упругих напряжений к кристаллу.
- Магнитостатической энергией магнетика, связанной с индуцированным магнитным полем поверхностными магнитными зарядами:
- Зеемановской энергией ферромагнетика во внешнем магнитном поле:
Таким образом, полная энергия состояния ферромагнитного кристалла является суммой всех вкладов, описанных выше и любой ферромагнитный кристалл стремится к минимизации полной энергии.
II. Образование доменной структуры в ферромагнетиках.
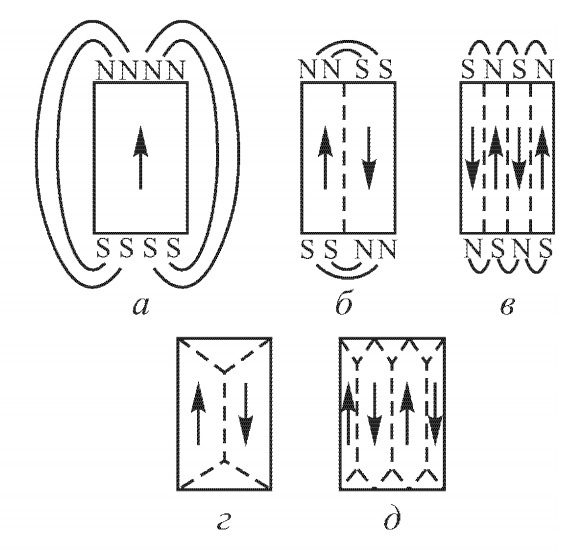
Рис. 1: Простейшие доменные структуры.
Рассмотрим идеальный ферромагнитный монокристалл, охлаждённый от точки Кюри без магнитного поля. Любые деформации и искажения решётки должны в нём отсутствовать. Если такой ферромагнитный монокристалл имеет форму бесконечно длинного стержня, с осью которого совпадает направление лёгкого намагничивания, то он, по-видимому, должен представлять собой один сплошной домен, т.е. все векторы спонтанного намагничивания в нём должны быть расположены параллельно друг другу и оси стержня. Действительно, энергия размагничивающего поля в этом случае равна нулю, так как равен нулю размагичивающий фактор $N$. Энергия анизотропии также минимальна, поскольку вектор намагниченности параллелен направлению оси легкого намагничивания (ОЛН). Минимальна и обменная энергия, так как все спины расположены параллельно друг другу. Всякое изменение однодоменности в этом случае вызвало бы увеличение хотя бы одного вида энергии, а следовательно привело бы ферромагнетик в неравновесное состояние. Реально подобный случай, по-видимому, может быть осуществлён в очень тонкой ферромагнитной плёнке (толщиной $\sim10^{-6}$ см).
У обычных кристаллов конечных размеров однодоменная магнитная структура (Рис. 1a) является энергетически невыгодной. Благодаря существованию размагничивающего поля $H_{P}=NI$ они обладают магнитостатической энергией (3). Энергетически выгодно разделение подобного кристалла на несколько доменов таким образом, чтобы соседние домены были намагничены антипараллельно, поскольку при этом уменьшается размагничивающий фактор $N$ (Рис. 1б,в). Чем на большее количество антипараллельных доменов разобьётся кристалл, тем меньше будет его магнитостатическая энергия. Эта энергия ещё больше снижается, если антипараллельно намагниченные домены перпендикулярно замыкаются намагниченным доменом (Рис. 1г,д). С другой стороны, между доменами создаются границы с антипараллельными спинами, и чем больше таких границ, тем больше величина их общей обменной энергии.
III. Переходные слои между доменами. Доменные границы.
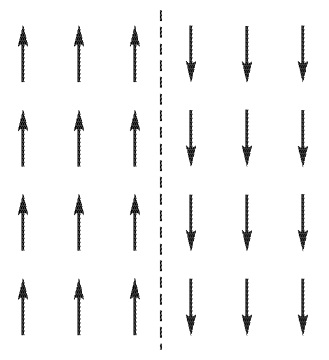
Рис. 2: Схема резкой границы между доменами.
Прежде чем выяснить, какая структура доменов является наиболее выгодной, посмотрим, что представляет собой переходный слой между ними. Для этого рассмотрим подробнее одноосный магнитный кристалл, т.е. ферромагнетик с одним направлением лёгкого намагничивания (например, кобальт). На границе между плоскими доменами векторы намагничивания изменяют своё направление на $180^\circ$ (от $I_s$ до $I_{-s}$). Если такой переход совершается между плоскостями кристалла, то он, не нарушая условия минимума энергии магнитной анизотропии, приводит к появлению большой положительной энергии обмена. Обменная энергия между двумя соседними антипараллельными спинами, согласно уравнению (1), равняется $2A_{ij}\sigma^2$. Поскольку у кристалла с постоянной решётки $a$ на один квадратный сантиметр границы с каждой стороны приходится $1/a^2$ спинов, то общая плотность обменной энергии на границе площадью 1 см$^2$ составляет (Рис. 2):
Если же граница между доменами представляет собой не резкий поворот соседних спинов на $180^\circ$, а плавный их поворот на протяжении большого числа спиновых слоёв (Рис. 3), то в плоскостях, параллельных поверхности раздела, величина обменной энергии, приходящейся на 1 см$^2$ границы, может быть существенно снижена.
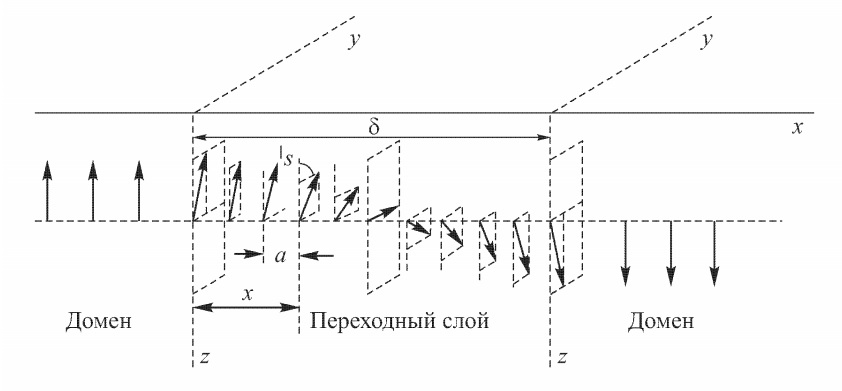
Рис. 3: Схема границы в виде переходного слоя.
Обозначим через $\theta$ угол между направлением лёгкого намагничивания и вектором намагниченности $\mathbf{I_s}$ в некоторой атомной плоскости переходного слоя на расстоянии $x$ от домена (Рис. 3), а через $\varphi$ – угол между спиновыми моментами соседних атомных слоёв, следовательно:
где $a$ – постоянная кристаллической решётки. Если угол $\varphi$ мал, то выражение для обменной энергии (1) примет вид:
В дальнейшем можно учитывать только зависящую от $\varphi$ часть обменной энергии – $2A_{ij}\sigma^2(\varphi^2/2)=A_{ij}\sigma^2\varphi^2$. Подставив это выражение в соотношение (6), получим обменную энергию в виде:
Если толщина доменной границы – $\delta$ (Рис. 3), а полный поворот спиновых моментов в переходном слое от одного домена к другому составляют $180^\circ=\pi$, то тогда $d\theta/dx=\pi/\delta$, и обменная энергия примет вид:
Число спинов в толще переходного слоя составляет $N=\delta/a$, а на 1 см$^2$ его поверхности приходится $1/a^2$ спиновых моментов. Поэтому плотность обменной энергии, приходящейся на 1 см$^2$ переходного слоя, равна:
Сравним выражения (5) и (10) получим, что энергия доменной границы при плавном повороте спиновых моментов вдоль её толщины в $\delta/\pi^2a$ раз меньше, чем при резком повороте. Из выражения (10) также видно, что обменная энергия тем меньше, чем больше толщина доменной границы, в котором осуществляется плавный поворот спинов. Таким образом, обменная энергия стремится увеличить толщину доменной границы. Если резкий поворот на угол $\pi$ никак не отражается на величине энергии магнитной анизотропии, поскольку в обоих соседних доменах векторы намагничивания направлены вдоль направления лёгкого намагничивания, то в случае границы в виде переходного слоя определённой ширины энергия магнитной анизотропии возрастает за счёт установления магнитных моментов в различных атомных слоях под отличными от нуля углами $\theta$ к направлению лёгкого намагничивания. А это означает, что энергия доменной границы $w_\delta$ складывается из обменной энергии (10), которая стремится увеличить ширину границы и энергии магнитной анизотропии, которая стремится наоборот её уменьшить.
Предположим для простоты, что векторы намагниченности по всей ширине доменной границы перпендикулярны к направлению лёгкого намагничивания. Тогда плотность энергии магнитной анизотропии на 1 см2 доменной границы равна $w_a=K_1\delta$, где $K_1$ – константа магнитной анизотропии. Если теперь учесть, что не все магнитные моменты в этом слое перпендикулярны направлению лёгкого намагничивания, а угол с направлением лёгкого намагничивания плавно меняется от одной границы к другой, то следует ввести некоторый коэффициент пропорциональности $\beta<1$. Тогда плотность энергии переходного слоя окажется равной $w_a=\beta K_1\delta$, т.е. энергия магнитной анизотропии прямо пропорциональна толщине доменной границы. Таким образом, для плотности общей энергии доменной границы получаем:
Толщину переходного слоя нужно искать из условий минимума энергии $w_{\delta}$:
т.е. искомая толщина обратно пропорциональная корню квадратному из константы анизотропии. Константа анизотропии при повышении температуры, как правило, уменьшается до нуля. Следовательно толщина доменной границы при повышении температуры растёт, а при температуре Кюри достигает значения $\delta\longrightarrow\infty$ (т.е. доменная структура пропадает).
Важно отметить, что при рассмотрении расположения спиновых моментов в доменной границе мы не учитывали возможности их поворота в плоскости расположения векторов намагничивания в соседних доменах (т.е. в плоскости, перпендикулярной поверхности границ). Дело в том, что такой способ изменения ориентации спиновых моментов в доменной границе менее выгоден, чем рассмотренный выше, при котором они изменяют свою ориентацию в плоскостях, параллельных границам. При изменении ориентации спинов в плоскости, перпендикулярной границам, кроме обменной энергии и энергии магнинтой анизотропии, добавляется энергия размагничивающего поля, имеющегося в доменной границе. В этом случае доменная граница будет представлять собой тонкий слой с размагничивающим фактором $N=4\pi$. При изменении ориентации спиновых моментов в плоскости, перпендикулярной границе, появляется составляющая намагниченности $I_p$ в этом направлении и, следовательно, размагничивающее поле. Дополнительная плотность энергии при этом будет составлять $w_p=4\pi I_p^2\delta$. Из сказанного следует, что энергетически выгодно, чтобы в рассмотренной выше 180-градусной доменной границе магнитные моменты оставались параллельными границе раздела между доменами. Такая граница впервые была исследована Ф. Блохом, поэтому её часто называют блоховской доменной границей.
Ситуация, когда вектору намагниченности становится энергетически более выгодно поворачиваться в плоскости перпендикулярной поверхности границ также имеет место, но реализуется она только в тонких плёнках толщиной порядка 100 нм или меньше. Эта ситуация была подробно исследована Л. Неелем, поэтому такие доменные границы часто называют неелевскими. В рамках данной задачи мы будем работать только с блоховскими доменными границами.
IV. Расчет ширины блоховской доменной стенки.
Результат, полученный в параграфе III, можно вывести в более строгом математическом виде. Как мы выяснили, на ширину доменной границы в основном влияют обменная энергия и энергия магнитной анизотропии. В магнитоодноосном кристалле локальная плотность энергии представляется в виде:
где $A$ и $K$ – константы обменного взаимодействия и магнитной анизотропии, $\theta$ – угол между осью легкого намагничивания и намагниченностью $\mathbf{I}$.
Равновесное распределение намагниченности в доменной границе отвечает минимуму энергии некоторого объёма кристалла $V$:
Функция $E(\theta)$, минимизирующая этот функционал, находится стандартным способом с помощью уравнения Эйлера, которое в нашем случае имеет вид:
Подставляя выражение для энергии $E$ получаем уравнение для функции $\theta(x)$:
Для граничных условий $\theta(-\infty)=0, \theta(\infty)=\pi$ находим решение:
Графически это распределение построено на Рис. 5. Дополнительно на графике мы построили функции $\theta=\pi$, и касательную к результирующей кривой в точке $x=0$. Теперь можно вычислить эффективную ширину доменной границы по пересечению касательной с функциями $\theta=0$ и $\theta=\pi$.
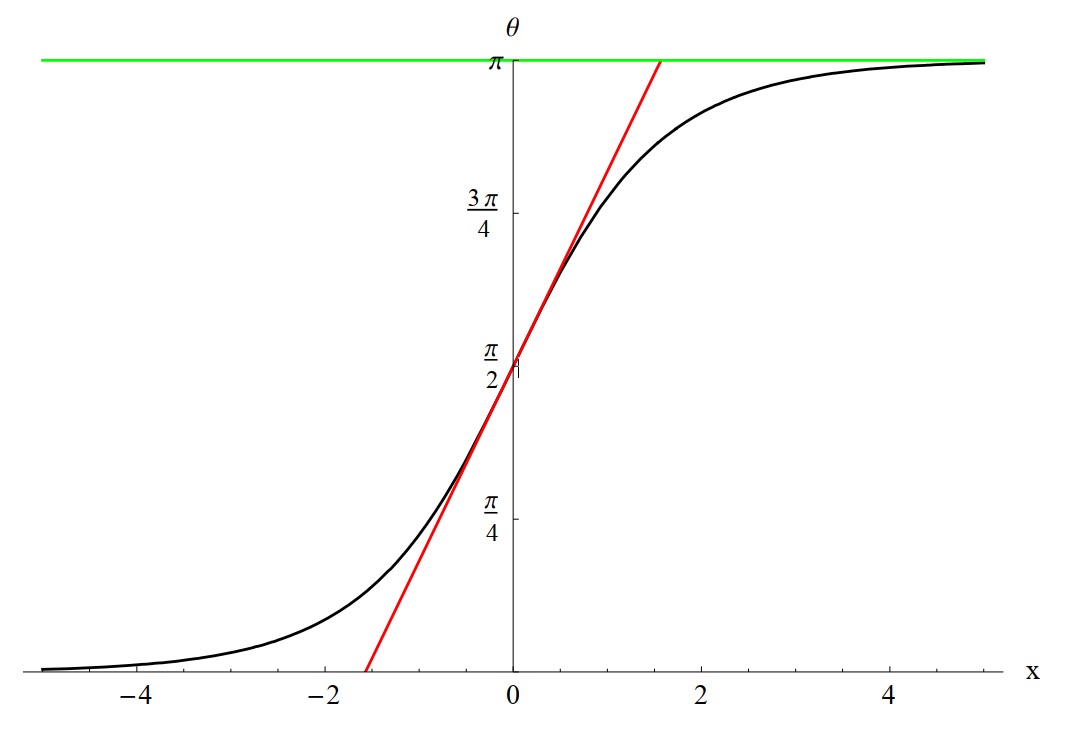
Рис. 9: Зависимость угла поворота намагниченности от координаты $\theta(x)$ в блоховской доменной границе.
Выполняя необходимые расчёты получаем выражение для эффективной ширины доменной границы:
Этот результат аналогичен тому, что был получен ранее в параграфе III.
Список литературы
- [1] В.С. Вонсовский, Магнетизм. Магнитные свойства диа-, пара-, ферро-, антиферро- и ферримагнетиков. Москва. 1971.
- [2] Alex Hubert, Rudolf Schäfer. Magnetic Domains. The Analysis of Magnetic Microstructures. Springer 2008.
- [3] Г. С. Кринчик. Физика магнитных явлений. Москва. 1976.
Вопросы к задаче
- Рассчитать эффективную ширину доменной границы в кобальте. Параметры: K=4.5*105 Дж/м3, A=1.3*10-11 Дж/м.
- Рассчитать эффективную ширину доменной границы в железе. Параметры: K=4.6*104 Дж/м3, A=2.5*10-11 Дж/м.
- Рассчитать эффективную ширину доменной границы в никеле. Параметры: K=5.0*103 Дж/м3, A=3.4*10-12 Дж/м.
- Рассчитать эффективную ширину доменной границы в ферритах-гранатах. Параметры: K=(3-40)*102 Дж/м3, A=(1-3)*10-12 Дж/м.
- По фотографиям, представленным на рисунках определить видимую ширину доменной границы.
Доменная структура кристалла 3% Si-Fe полученная методом Биттера [2]
Масштаб: 0 нм/пикс, Длина отрезка: нм
Доменная структура кристалла 3% SiFe полученная методом Керра [2]
Масштаб: 0 нм/пикс, Длина отрезка: нм
Доменная структура кристалла SiFe с ориентацией (100) полученная с помощью эффекта Керра при вертикальной плоскости падения [2]
Масштаб: 0 нм/пикс, Длина отрезка: нм
Доменная структура малой частицы пермаллоя толщиной 24 нм, полученной с помощью метода просвечивающей электронной микроскопии [2]
Масштаб: 0 нм/пикс, Длина отрезка: нм
Доменная структура на поверхности железного провода. Изображение получено методом сканирующей электронной микроскопии [2]
Масштаб: 0 нм/пикс, Длина отрезка: нм
Доменная структура малой частицы пермалоя
Масштаб: 0 нм/пикс, Длина отрезка: нм
Доменные границы в тонкопленочном элементе Fe (толщина 30 нм), полученные с помощью магнитной силовой микроскопии [2]
Масштаб: 0 нм/пикс, Длина отрезка: нм
Лабиринтная доменная структура в пленке феррита-граната
Масштаб: 0 нм/пикс, Длина отрезка: нм