ПЕРИОДИЧЕСКИЙ ПОТЕНЦИАЛ. ТЕОРЕМА БЛОХА.
Оглавление
- I. Теорема Блоха.
- II. Модель Кронига-Пенни.
- III. Дираковская потенциальная гребёнка.
- IV. Периодические потенциальные барьеры.
- Вопросы к задаче.
- Список литературы.
- Калькулятор.
I. Теорема Блоха
В любом металле газ свободных электронов не является абсолютно идеальным. Электроны взаимодействуют как между собой, так и с ионами кристаллической решётки. Поэтому, теории металлов, основанные на приближении свободных электронов (Друде и Зоммерфельда), не всегда дают точные предсказания для электрических и термодинамических свойств некоторых материалов. Отсюда следует необходимость учёта потенциала кристаллической решётки, который меняет свойства свободного электрона.
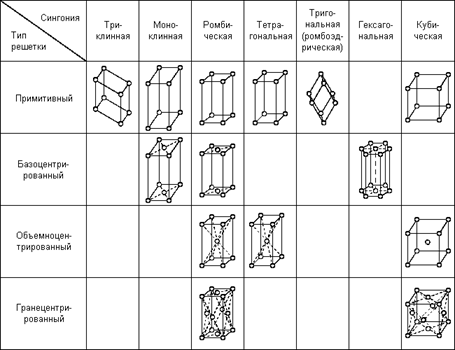
Рис. 1: Решетки Браве [1].
В идеальном бесконечном кристалле соблюдается строгая периодичность расположения атомов, которая определяется решеткой Браве. Общее количество всевозможных решёток Браве равно 14 (Рис. 1). При этом, потенциал, в котором будут находиться электроны также будет обладать данной периодичностью:
где R – вектор решетки Браве или вектор трансляции. Плотность электронов в точке r, определяемая как квадрат модуля волновой функции электрона |ψ(r)|^2, в силу периодичности потенциала тождественна плотности электронов в точке r+R. Значит волновая функция в точке r может отличаться от волновой функции в точке r+R только на фазовый множитель, зависящий от вектора трансляции R:
где k – волновой вектор электрона в периодическом потенциале (1) или блоховского электрона. Выражение (2) называется теоремой Блоха, согласно которой волновые функции одноэлектронного гамильтониана, содержащего периодический потенциал U(r) можно записать в виде:
где $u_n(\mathbf{r})=u_n(\mathbf{r+R})$ – некая периодическая функция, $n\in[0,\infty)$ – номер решения, или номер зоны Бриллюэна. Нетрудно видеть, что выражения (2) и (3) эквивалентны.
Из теоремы Блоха следует, что волновая функция электрона периодична в обратном пространстве с периодом равным произвольному вектору обратной решетки K. Это вытекает из выражения (2), так как по определению обратной решетки $e^{i\mathbf{KR}}=1$. Но если волновая функция блоховского электрона периодична в обратном пространстве, то и его энергия также периодична с этим же периодом $\varepsilon_n(\mathbf{k})=\varepsilon_n(\mathbf{k+K})$. Поэтому расчет закона дисперсии блоховского электрона $\varepsilon_n(k)$ достаточно проводить только для первой зоны Бриллюэна.
II. Модель Кронига-Пенни
Модель Кронига-Пенни является простейшей моделью электронной структуры одномерного кристалла. В этой модели периодический потенциал представляется в виде прямоугольных потенциальных ям шириной a и прямоугольных потенциальных барьеров шириной b (период a+b) и высотой V0, как это изображено на Рис. 2.
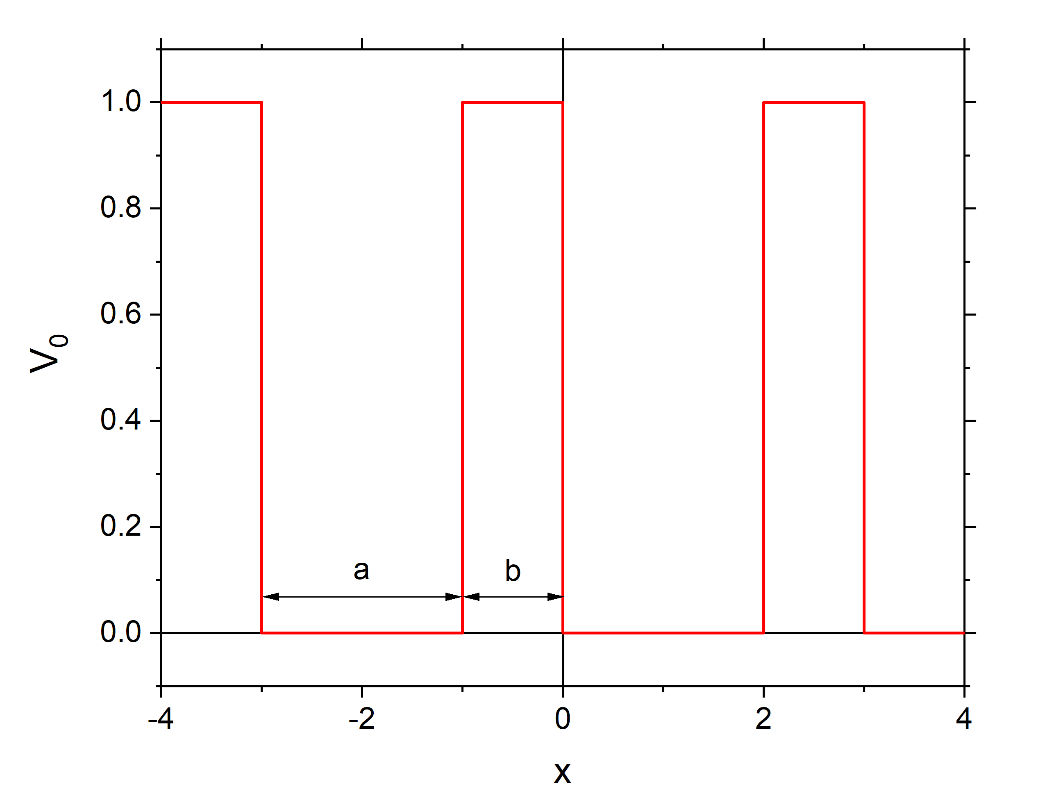
Рис. 2: Периодический потенциал из прямоугольных барьеров.
III. Дираковская потенциальная гребёнка
Если $b\to0$ и $V_0\to\infty$ так, что $bV_0=\hbar^2\Omega/m$, где параметр $\Omega$ имеет размерность волнового вектора, то потенциал в модели Кронига-Пенни называют дираковской потенциальной гребёнкой, и его записывают в виде:
где a – период решётки. На интервале $x\in(0,a)$ волновая функция электрона с энергией E является суперпозицией набегающих и отражённых плоских волн:
где A и B – неизвестные коэффициенты, $\kappa=\sqrt{2mE/\hbar^2}$ – волновой вектор свободного электрона с энергией E. Из теоремы Блоха следует, что волновая функция на соседнем интервале $x\in(a,2a)$ будет отличаться на фазовый множитель $e^{ika}$:
где k – неизвестный волновой вектор блоховского электрона в периодическом потенциале.
Условия «сшивания» на границе x=a дают систему уравнений:
\[\left.\frac{\partial\psi_2(x)}{\partial x}\right|_{x=a}=\left.\frac{\partial\psi_1(x)}{\partial x}\right|_{x=a}+2\Omega\psi_1(a) ,\]
или:
\[e^{ika}(A-B)=Ae^{i\kappa a}-Be^{-i\kappa a}-i\frac{2\Omega}{\kappa}(Ae^{i\kappa a}+Be^{-i\kappa a}) ,\]
Нетрудно убедиться, что решение для $e^{ika}$ будет являться решением квадратного уравнения:
Действительная часть решения равная $\cos{k a}$ не должна превышать по модулю значения 1, следовательно можно записать условие для допустимых значений волнового вектора свободного электрона $\kappa$ и энергии $E$:
Результат представлен на Рис. 3 при a=3 Å, Ω=3 Å-1.
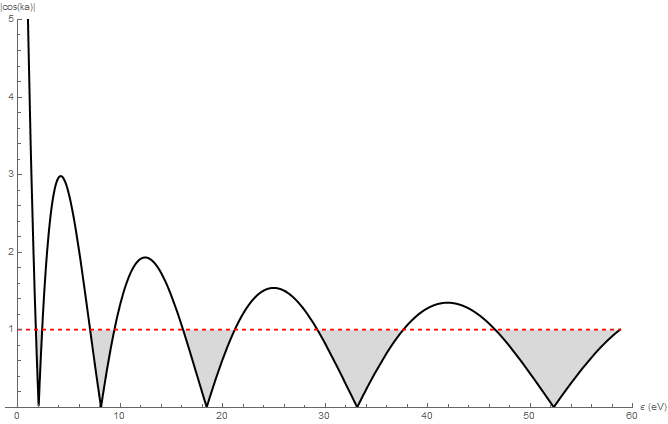
Рис. 3: Области разрешенных (≤1) и запрещённых (>1) значений энергий электрона E, определяемые соотношением (10).
Из уравнения:
видно, что волновой вектор блоховского электрона k совпадает с волновым вектором свободного электрона $\kappa$, также как и их энергии, при условии $\kappa a=\pi n$. В остальных случаях они различаются. Если искать решение этого трансцендентного уравнения относительно импульса $\kappa_n$, где n определяет интервал значений $[\pi n,\pi(n+1)]$, для произвольного ka на интервале $[-\pi,\pi]$ и построить зависимость энергии $E_n=\hbar^2 \kappa_n^2/(2m)$ от $ka$ (закон дисперсии), то можно увидеть области разрешенных и запрещенных энергий для электрона в периодическом потенциале (Рис. 4). Закон дисперсии блоховского электрона уже не является квадратичным, как в случае свободных электронов. Таким образом, он превращается в квазичастицу со своим законом дисперсии и эффективной массой, не равной массе свободного электрона.
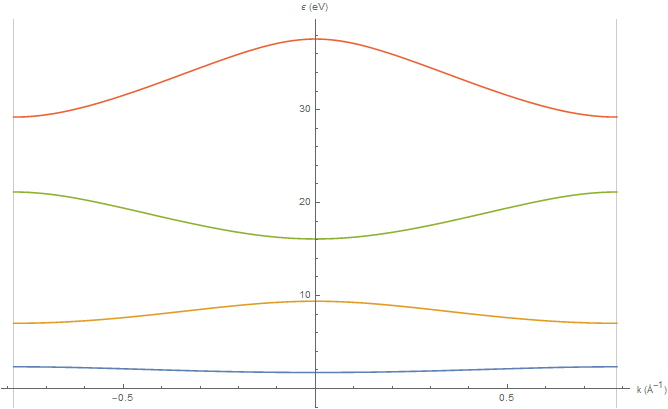
Рис. 4: Зависимость энергии электрона в периодическом потенциале от k для первой зоны Бриллюэна и трёх первых энергетических зон (схема приведённых зон).
Если устремить параметр Ω к нулю (предел свободных электронов), то энергетические зоны начнут расширяться, а барьеры между ними исчезать. При этом, закон дисперсии будет стремиться к квадратичному. Если, наоборот, устремить Ω к бесконечности (предел сильной связи), то энергетические барьеры будут увеличиваться, а разрешённые значения энергии будут сужаться до дискретных значений в точках $\kappa a=\pi n$.
IV. Периодические потенциальные барьеры
Для примера рассмотрим теперь периодический потенциал следующего вида: прямоугольные потенциальные барьеры высотой V0, шириной b и расстоянием между ними a (Рис. 2).
Запишем искомые волновые функции электронов внутри области (индекс b) и вне области (индекс w) барьеров:
\[\psi_{w1}=A_w e^{i\kappa x}+B_w e^{-i\kappa x} ,\]
где $q^2=2m(V_0-E)/\hbar^2$, $E\lt V_0$, $\kappa^2=2mE/\hbar^2$. Тогда, согласно теореме Блоха, волновые функции в соседней области, смещённой на шаг a+b будут иметь вид:
\[\psi_{w2}=e^{ik(a+b)} (A_w e^{i\kappa(x-a-b)}+B_w e^{-ı\kappa(x-a-b)}).\]
Условия «сшивания» на границах самих функций и их производных в точках x=0 и x=a приводят к системе уравнений:
\[\psi_{w1} (a)=\psi_{b2} (a), \psi_{w1}'(a)=\psi_{b2}'(a) .\]
Или:
\[q(A_b-B_b )=i\kappa(A_w-B_w ) ,\]
\[ e^{ik(a+b)} (A_b e^{-qb}+B_b e^{qb} )=A_w e^{i\kappa a}+B_w e^{-i\kappa a} ,\]
\[ e^{ik(a+b)} q(A_b e^{-qb}-B_b e^{qb} )=i\kappa(A_w e^{i\kappa a}-B_w e^{-i\kappa a} ).\]
Решение получившейся однородной системы линейных уравнений относительно коэффициентов $A_b$, $B_b$, $A_w$, $B_w$ даёт тривиальный нулевой результат. Условие существования нетривиального решения такой системы – это равенство нулю её определителя:
Решение уравнения (16) даёт выражение для волнового вектора блоховского электрона k:
Следовательно, условие для допустимых значений волнового вектора свободного электрона $\kappa$:
Решение трансцендентного уравнения (17) относительно энергии $E_n=\hbar^2 \kappa_n^2/(2m)$, где $n$ определяет энергетическую зону, для произвольного $k(a+b)$ на интервале $[-\pi,\pi]$ (первая зона Бриллюэна) даст закон дисперсии блоховского электрона в данном периодическом потенциале. Но задача, по сравнению с первым примером, осложняется тем, что периоды левой и правой частей уравнения не совпадают, так как присутствует экспоненциальный множитель в виде гиперболической функции. Тем не менее, задача решается численно, и результаты для первых четырёх энергетических зон для случая a=4 Å, b=1 Å, V0=3 эВ в первой зоне Бриллюэна представлены на Рис. 5 (схема приведённых зон). Если транслировать кривые энергий в приведенной схеме на соседние зоны Бриллюэна, то в результате получится периодическая зонная схема, изображенная на Рис. 6. Кроме этих двух схем, представленных на Рис. 5 и Рис. 6, различают ещё одну (Рис. 7), где различные энергетические зоны размещены в обратном пространстве в различных зонах Бриллюэна (расширенная зонная схема), из которой видно, что при больших значениях волнового вектора ($k\gg 2mV_0/\hbar^2$) закон дисперсии стремится к квадратичному пределу свободного электрона. Нетрудно убедиться, что если V0=0, то решением будет являться $k=\kappa$ (предел свободных частиц).
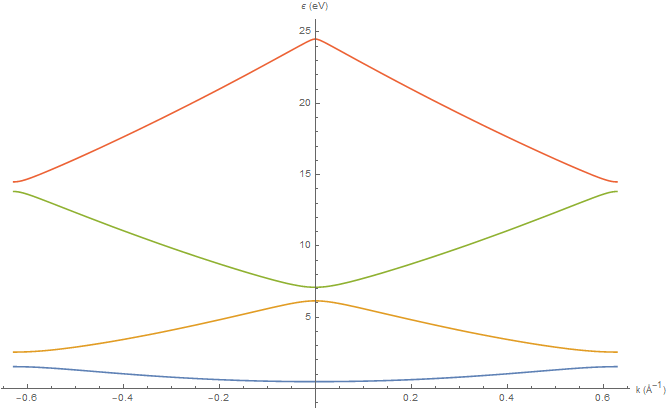
Рис. 5: Зависимость энергии электрона в периодическом потенциале от k для четырёх первых энергетических зон в первой зоне Бриллюэна (схема приведённых зон). Параметры задачи: a=4Å, b=1Å, V0=3 эВ.
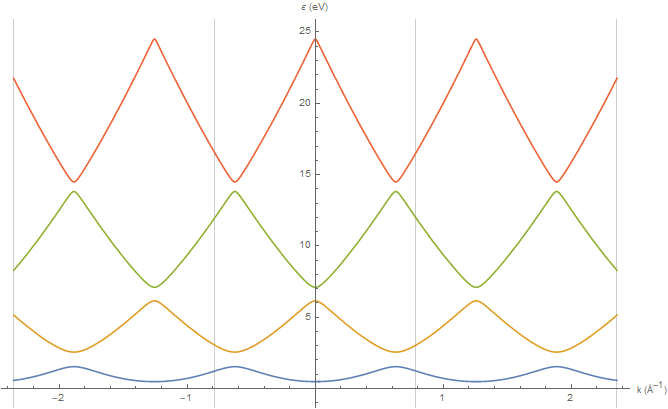
Рис. 6: Зависимость энергии электрона в периодическом потенциале от k для четырёх первых энергетических зон в трёх зонах Бриллюэна (схема периодических зон). Параметры задачи как на Рис. 5.
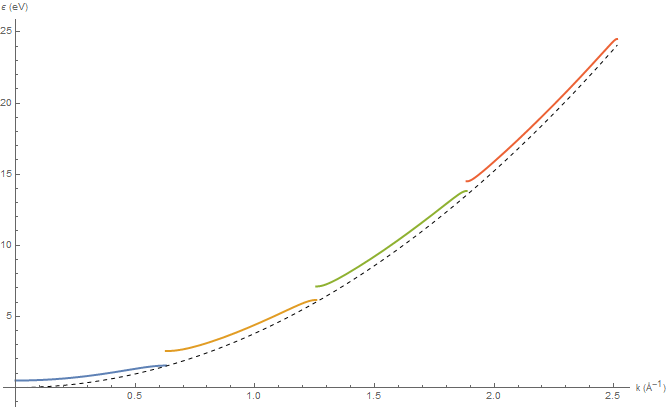
Рис. 7: Зависимость энергии электрона в периодическом потенциале от k для первых четырёх энергетических зон и зон Бриллюэна, расположенных друг за другом (расширенная зонная схема). Штриховая линия соответствует квадратичному закону дисперсии свободного электрона. Параметры задачи как на Рис. 5
Вопросы к задаче
- Рассчитайте энергетическую щель между первой и второй энергетической зоной для электрона в периодическом δ–образном потенциале с параметрами a=3 Å, Ω=4 Å.
- На сколько отличается энергия электрона в периодическом δ–образном потенциале с параметрами a=3 Å, Ω=4 Å в центре зоны Бриллюэна в первой и второй энергетической зоне от энергии свободного электрона.
- Рассчитайте разницу между шириной первой энергетической зоны в периодическом δ–образном потенциале с параметрами a=3 Å, Ω=4 Å и a=3 Å, Ω=20 Å.
Список литературы
- [1] Б.К. Вайнштейн, Современная кристаллография, т.1, М. Наука, 1979.
- [2] Н. Ашкрофт, Н. Мермин, Физика твердого тела, т.1, М. Мир, 1979.
- [3] Дж. Займан, Принципы теории твёрдого тела, М. Мир, 1966.
- [4] Ч. Киттель, Введение в физику твёрдого тела, М. Наука, 1978.