Магнитное поле однослойного соленоида
Соленоид – это цилиндрическая обмотка из провода по которой протекает постоянный или переменный электрический ток. Обмотка может наноситься в один или несколько слоёв виток к витку. Если длинна соленоида значительно превышает его диаметр, то поле, создаваемое постоянным током сосредоточено внутри него и практически однородно.
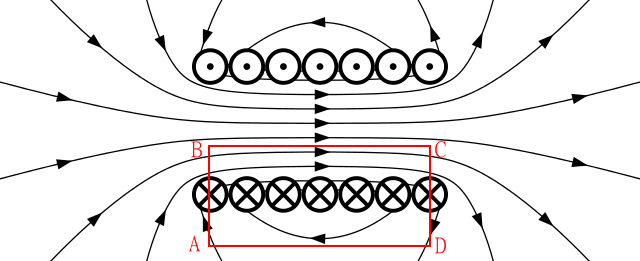
Рис. 1: Магнитное поле, создаваемое серией кольцевых токов
Для вычисления индукции магнитного поля $\vec B$ внутри однослойного соленоида представим его в виде суперпозиции кольцевых токов лежащих на одной оси – оси соленоида (Рис. 1) и воспользуемся теоремой о циркуляции:
Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая приближение однородности поля получим:
где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:

Рис. 2: Соленоид с произвольными размерами $L$ и $R$.
Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:
В частном случае, в середине соленоида, где магнитное поле максимально выражение для индукции будет иметь вид:
где $R$ – радиус соленоида. А на краю полубесконечного соленоида: